[백준/C++] #11057 오르막 수 (DP)
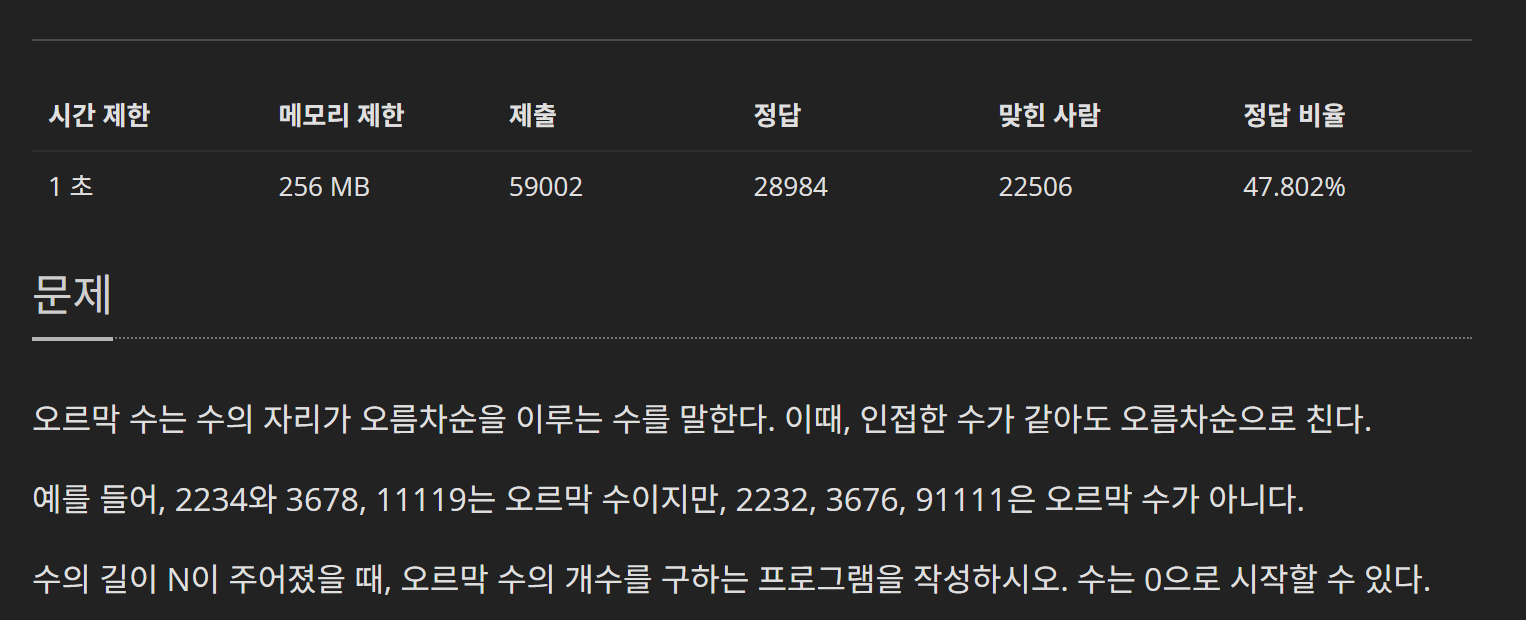
문제
https://www.acmicpc.net/problem/11057

풀이
1. 팩토리얼 사용해서 integerOverflow 발생한 코드
: 팩토리얼을 계산하는 과정에서 숫자가 매우 커지기 때문에 long long으로도 수를 감당할 수 없게 되어 integerOverflow 발생
사용할 수의 개수만큼 0~9중에 고르기 & 마지막 자릿수 제외한 자릿수 중에 어디"까지" 특정 수가 나올지 고르기
이렇게 두 로직을 combination으로 계산할 수 있다.
예를 들면,
수의 길이가 4라고 하자.
길이가 4인 수는 숫자 4개 혹은 3개 혹은 2개 혹은 1개로 오르막 수를 구성할 수 있다.
숫자 4개를 이용하는 수를 만들기 위해서는 0~9 수들 중 중복되지 않는 수 4개를 고르고(10 C 4), 마지막 자리를 제외한 3자리를 구하면(3 C 3)된다. -> (10 C 4) * (3 C 3)
숫자 3개를 이용하는 수를 만들기 위해서는 0~9 수들 중 중복되지 않는 수 3개를 고르고 (10 C 3), 마지막 자리를 제외한 2자리를 구하면 (3 C 2)된다. -> (10 C 3) * (3 C 2)
숫자 2개를 이용하는 수를 만들기 위해서는 0~9 수들 중 중복되지 않는 수 2개를 고르고 (10 C 2), 마지막 자리를 제외한 1자리를 구하면 (3 C 1)된다. -> (10 C 2) * (3 C 1)
숫자 1개를 이용하는 수를 만들기 위해서는 0~9 수들 중 중복되지 않는 수 1개를 고르고 (10 C 1), 마지막 자리를 제외한 0자리를 구하면 (3 C 0)된다. -> (10 C 1) * (3 C 0)
이렇게 나온 계산의 결과값들을 모두 더하면, 답이 나온다.
(10 C 4) * (3 C 3) + (10 C 3) * (3 C 2) + (10 C 2) * (3 C 1) + (10 C 1) * (3 C 0) = 715
#include<iostream>
#include<algorithm>
#define endl "\n"
#define MOD 10007
using namespace std;
int res = 0;
int len;
long long factorial(int b) {
long long result = 1;
for (int i = 2; i <= b; i++) {
result *= i;
}
return result;
}
long long fac(int a, int b) {
long long result = 1;
for (int i = 1; i <= b; i++) {
result *= a--;
}
return result;
}
int combination(int a, int b) {
return (fac(a, b) / factorial(b)) % MOD;
}
void solution() {
for (int i = 1; i <= len; i++) {
int comb1 = combination(10, i) % MOD;
int comb2 = combination(len - 1, i - 1) % MOD;
res = (res + (comb1 * comb2) % MOD) % MOD;
}
}
int main() {
ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
// 입력
cin >> len;
// 로직
solution();
// 출력
cout << res % MOD;
return 0;
}나름 수학적으로 시도해본건데.. integerOverflow네 칫
DP 사용한 코드
길이가 4인 수는 길이가 3인 수에서 마지막 자리만 늘어난 꼴임.
예를 들자면,
| 길이 2. 마지막 자리 각각 0, 1, 2 | 길이 3. 마지막 자리 0 | 길이3. 마지막 자리1 | 길이3. 마지막 자리2 |
| 00 01 11 02 12 22 |
000 |
001 011 111 |
002 012 112 022 122 222 |
행: 길이 / 열: 끝나는 숫자의 값 / 행렬 값 : 오르막 수의 개수
0 1 2 3 4 5 6 7 8 9
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 |
| 1 | 4 | 10 | 20 | 35 | 56 | 84 | 120 | 165 | 220 |
| ... |
#include <iostream>
#define MOD 10007
using namespace std;
int dp[1001][10];
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
int len;
cin >> len;
// 초기화: 길이가 1일 때, 각 숫자로 끝나는 오르막 수의 개수는 1개씩
for (int i = 0; i <= 9; i++) {
dp[1][i] = 1;
}
// DP 테이블 채우기
for (int i = 2; i <= len; i++) { // 길이
for (int j = 0; j <= 9; j++) { // 마지막 숫자
dp[i][j] = 0; // 초기화
for (int k = 0; k <= j; k++) { // 이전 자리 숫자
dp[i][j] = (dp[i][j] + dp[i - 1][k]) % MOD;
}
}
}
// 결과 계산
int result = 0;
for (int i = 0; i <= 9; i++) {
result = (result + dp[len][i]) % MOD;
}
cout << result << "\n";
return 0;
}