문제
https://www.acmicpc.net/problem/1509

구상
확실히 골드 1이 느껴지는 문제였다. 그래도 차근차근 접근하니 옳은 풀이까지 도달할 수 있었다.
역시나 DP말고 특별한 접근 방식이 떠오르지 않아서 DP로 접근을 했다. 작은 길이의 팰린드롬 분할의 개수의 최솟값을 통해 더 큰(긴) 팰린드롬 분할의 개수의 최솟값을 구할 수 있었다.
그래서 처음에는 흔한 다른 DP문제들과 유사하게 접근을 했다. 흔한 DP 문제들은 DP배열의 특정 값이 답이 되는데, 그래서 나도 DP[i][j]가 str[i]~str[j]문자열에서 팰린드롬 분할의 개수의 최솟값이라고 잡고 문제를 접근했다. 그런데, 특정 크기의 문자열이 팰린드롬인지 확인하는 로직이 필요했다. 팰린드롬 여부를 어떻게 확인할까? 생각하다가, 여부 판단하는 로직도 dp로 풀이가 가능했다. 그래서 isPalindrom[s][e]라는 str[s]~str[e] 문자열의 팰린드롬 여부를 확인하는 배열을 사용했다. 역시나 e-s 크기를 가장 큰 기준으로 두어 문자열 길이가 1일때, 2일때, 3이상일때로 나누어 따로 갱신했다. 이렇게 팰린드롬 여부를 구한 이후, 팰린드롬 분할의 개수의 최솟값을 구해야 했다. dp를 이용해서 풀이를 써봤다. 아래 첫번째 사진의 맨 아래 로직인데, for 문자열의 길이 { for 시작 위치 { for 분할 위치 dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + 1) }} 를 생각했었다. 그런데, 역시나 3중 for문을 사용해 O(N^3)이 되어 시간 초과가 났다.
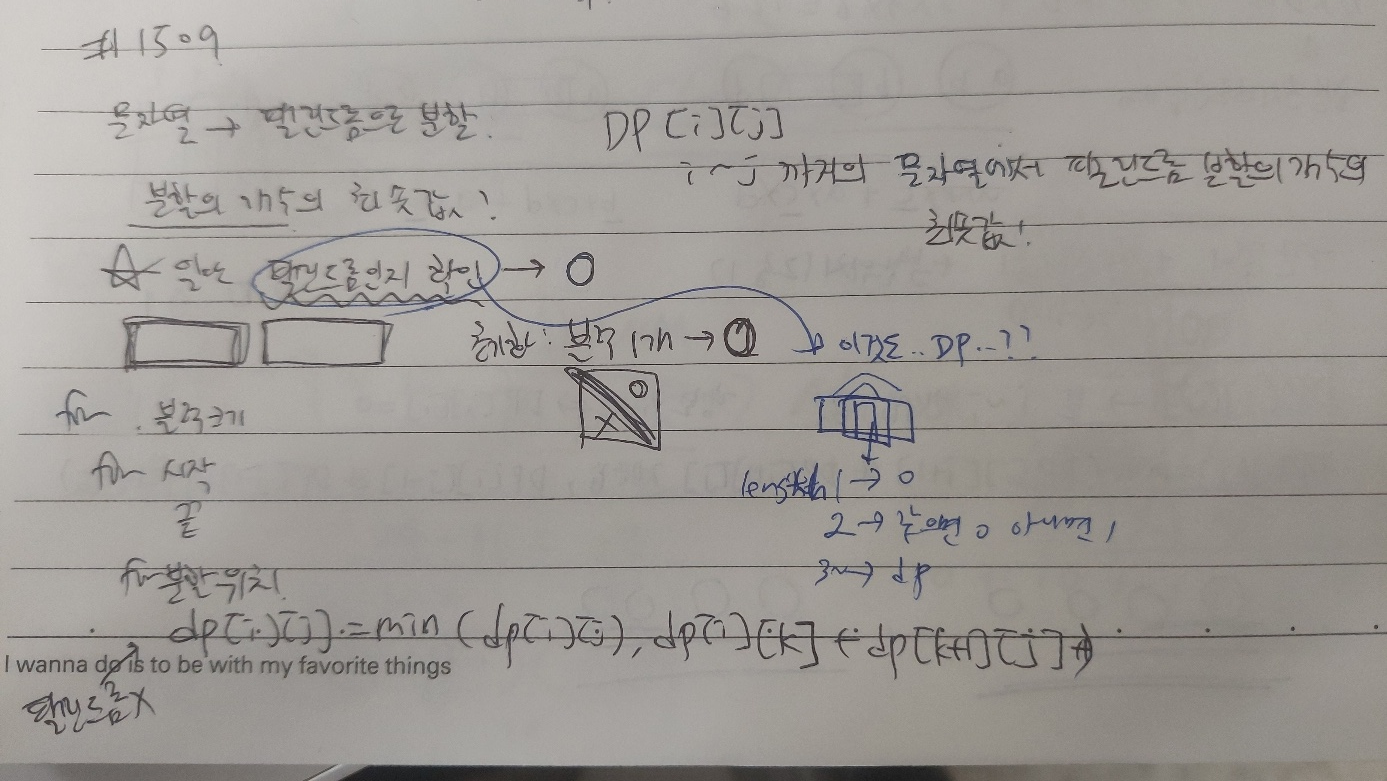
그래서 2차원 dp 배열로는 시간복잡도를 줄일 수 없다 판단하고, 2중 for문으로 풀 수는 없을까? 고민하다가, 그냥 문자열의 시작 위치를 고려하지 않기로 했다. 1차원인 dp배열에서 dp[i]는 str[0]~str[i] 문자열의 팰린드롬 분할 개수의 최솟값을 의미하도록 했다. 이렇게 마지막 위치랑 분할 위치만 고려하여 O(N^2)인 풀이를 작성해냈더니 정답이었다!

DP문제에서는 기준값으로 항상 "영역 크기", 시작값/끝값, 분할 위치를 생각하자!!
기준만 잘 잡아도 80% 성공이다.
알고리즘
이전의 계산값을 이용하여 더 큰 범위의 다음 값을 도출할 수 있으니 DP!!
풀이 + 코드
1. 시간 초과 나는 2차원 dp 사용한 풀이
#include<iostream>
#include<vector>
#include<algorithm>
#define MAX 2501
#define INF 987654321
#define endl "\n"
using namespace std;
int main() {
ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
// 입력
string str;
cin >> str;
int len = str.size();
// 로직
vector<vector<bool>> isPalindrome(len, vector<bool>(len, false)); // 팰린드롬 여부 저장
vector<vector<int>> dp(len, vector<int>(len, MAX)); // 최소 분할 횟수 저장
// 팰린드롬 여부 판단
for (int i = 0; i < len; i++) {
isPalindrome[i][i] = true; // 길이 1
}
for (int i = 0; i < len-1; i++) {
if (str[i] == str[i+1]) isPalindrome[i][i+1] = true; // 길이가 2
}
for (int length = 3; length <= len; length++) { // 길이 3 이상
for (int s = 0; s <= len - length; s++) { // 시작 값
int e = s + length - 1; // 끝 값
if (str[s] == str[e] && isPalindrome[s+1][e-1]) {
isPalindrome[s][e] = true;
}
}
}
// dp 초기화
for (int i = 0; i < len; i++) {
dp[i][i] = 0; // 길이 1
}
// dp 값 계산
for (int length = 2; length <= len; length++) {
for (int s = 0; s <= len - length; s++) {
int e = s + length - 1;
if (isPalindrome[s][e]) {
dp[s][e] = 0; // 팰린드롬이면 분할 필요 없음
} else {
for (int k = s; k < e; k++) {
dp[s][e] = min(dp[s][e], dp[s][k] + dp[k+1][e] + 1);
}
}
}
}
cout << dp[0][len - 1] << endl;
return 0;
}
2. 작은 시간복잡도를 갖는 1차원 dp배열을 사용한 풀이 (정답)
#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
#define MAX 2501
#define INF 987654321
#define endl "\n"
using namespace std;
/*
1509 팰린드롬 분할
*/
int main() {
ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
// 입력
string str;
cin >> str;
int len = str.size();
// 로직
vector<vector<bool>> isPalindrome(len, vector<bool>(len, false)); // false로 초기화
vector<int> dp(len, MAX);
// 팰린드롬 여부 판단 - 길이가 큰 기준
for (int i = 0; i < len; i++) {
isPalindrome[i][i] = true; // 길이 1
}
for (int i = 0; i < len-1; i++) {
if(str[i] == str[i+1]) isPalindrome[i][i+1] = true; // 길이가 2
}
for (int length = 3; length <= len; length++) { // 길이 3 이상
for (int s = 0; s <= len - length; s++) { // 시작 값
int e = s + length - 1; // 끝 값
if(str[s] == str[e] && isPalindrome[s+1][e-1]) isPalindrome[s][e] = true;
}
}
// dp[i]: str[0]~str[i]문자열의 팰린드롬 분할 횟수의 최솟값
for (int i = 0; i < len; i++) {
if (isPalindrome[0][i]) dp[i] = 0; // 처음부터 i까지가 팰린드롬이면 분할 필요 없음
else {
dp[i] = i; // 최악의 경우
for (int j = 0; j <= i; j++) {
if (isPalindrome[j][i]) dp[i] = min(dp[i], dp[j - 1] + 1); // 이전값 사용
}
}
}
cout << dp[len - 1] + 1; // 블럭 수니까 + 1
return 0;
}
'알고리즘 > BOJ' 카테고리의 다른 글
| [백준/C++] #10026 적록색약 (BFS/DFS - Flood Fill) (1) | 2024.07.31 |
|---|---|
| [백준/C++] #16933 벽 부수고 이동하기 2, 3 (BFS) (0) | 2024.07.31 |
| [백준/C++] #11049 행렬 곱셈 순서 (DP) (0) | 2024.07.23 |
| [백준/C++] #11066 파일 합치기 (DP) (2) | 2024.07.23 |
| [백준/C++] #2293 동전1 (DP) (3) | 2024.07.22 |



